Chih-Hao Fang

Chih-Hao Fang

Applied Scientist @ Amazon | Purdue University.

Instrumental Variable

1 minute read

Published:

Preliminary

  • Sample Mean \(\mu_X\) :

    \[\begin{align} \mu_X = \frac{1}{N}\sum^N_{i=1}x_i \label{eq1}\tag{1} \end{align}\]

  • Standard deviation \(\sigma_X\) :

\[\begin{align} \sigma_X = \sqrt{\bf{E}[ {(X-\mu_x)}^2 ]} \\= \sqrt{\frac{1}{N} \sum^N_{i=1}(x_i-\mu_X)^{2} } \label{eq2}\tag{2} \end{align}\]
  • Covariance \(COV_{XY}\):
\[\begin{align} COV_{XY} = \bf{E}[ {(X-\mu_X) (Y-\mu_Y) } ] \label{eq3}\tag{3} \end{align}\]
  • Correlation \(r_{XY}\) :
\[\begin{align} r_{XY} = \frac{COV_{XY}}{\sigma_X\sigma_Y} =\frac{\bf{E}[ {(X-\mu_X) (Y-\mu_Y) } ]} {\sigma_X\sigma_Y} \\ = \frac{\sum^N_{i=1}(x_i-\mu_X)(y_i-\mu_Y)} { N \sigma_X\sigma_Y }\\=\frac{\sum^N_{i=1}(x_i-\mu_X)(y_i-\mu_Y)} { \sqrt{ \sum^N_{i=1}(x_i-\mu_X)^{2} \sum^N_{i=1}(y_i-\mu_Y)^{2} } } \label{eq4}\tag{4} \end{align}\]

  • Slope of OLS \(\min_{\beta_0,\beta_1} \sum^N_{i=1}(y_i-\beta_0 - \beta_1x_i)^2\) :

    \[\begin{align} \beta_1 = \frac{dy}{dx}= \frac{\sum^N_{i=1} (x_i-\mu_X) (y_i-\mu_Y) }{\sum^N_{i=1} (x_i -\mu_X)^2 } \label{eq5}\tag{5} \end{align}\]

Instrumental Variable

IV

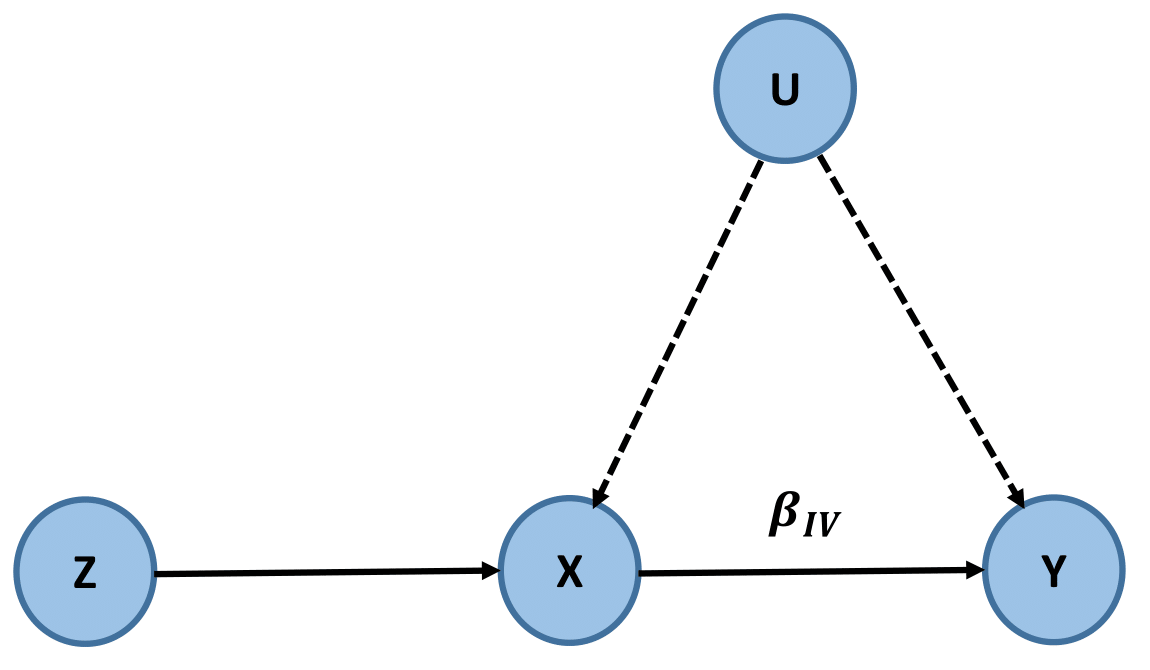
Definition of IV:

  • The IV \(Z\) is only associated with the exposure \(X\).
  • The IV \(Z\) is not associated with the unobserved confounder \(U\) of the exposure \(X\) and the outcome \(Y\).

Estimation of \(\beta_{IV}\):

\[\begin{align} y=\beta_{IV}x+\mu \label{eq6}\tag{6} \end{align}\]

Multiply \(\frac{1}{z}\) for both sides of (\ref{eq6})

We get

\[\begin{align} \frac{y}{z}= \beta_{IV} \frac{x}{z} +\frac{\mu}{z} \label{eq7}\tag{7} \end{align}\]

If we calculate the derivative with respective to \(z\), we have

\[\begin{align} \frac{dy}{dz}= \beta_{IV} \frac{dx}{dz} +\frac{d\mu}{dz} \label{eq8}\tag{8} \end{align}\]

Since \(\mu\) is uncorrelated with \(z\), we have the following estimate

\[\begin{align} \beta_{IV} = \frac{dy/dz}{dx/dz} \label{eq9}\tag{9} \end{align}\]

Plugin (\ref{eq5}), (\ref{eq4}), and (\ref{eq3}) into (\ref{eq9}), we have

\[\begin{align} \beta_{IV} &= \frac{dy/dz}{dx/dz} \\ &= \frac{\sum^N_{i=1} (z_i-\mu_Z) (y_i-\mu_Y) }{\sum^N_{i=1} (z_i -\mu_Z)^2 } \frac{\sum^N_{i=1} (z_i -\mu_Z)^2}{\sum^N_{i=1} (z_i-\mu_Z) (x_i-\mu_X)} \\ &= \frac{\sum^N_{i=1} (z_i-\mu_Z) (y_i-\mu_Y) }{\sum^N_{i=1} (z_i-\mu_Z) (x_i-\mu_X) } \\&= \frac{COV_{ZY}}{COV_{ZX}} \\&= \frac{r_{ZY}\sigma_Y} {r_{ZX}\sigma_X} \label{eq10}\tag{10} \end{align}\]

Interpretation of \(\beta_{IV}\) :

  • The change in the \(Y\) for a unit change in the \(X\) is equal to the change in \(Y\) for a unit change of \(Z\) scaled by the change in \(X\) for a unit change of \(Z\).

References

You May Also Enjoy